How To Find The Distance Between Two Points Calculator

Have you ever wanted to calculate the distance from one point to another, or the distance betwixt cities? Have you lot ever wondered what the distance definition is? We accept all these answers and more, including a detailed caption of how to summate the distance between any two objects in 2D space. As a bonus, nosotros accept a fascinating topic on how we perceive distances (for instance equally a percentage deviation); nosotros're sure you'll dear information technology!

What is distance?

Before we get into how to summate distances, we should probably clarify what a altitude is. The nearly common meaning is the /1D infinite betwixt ii points. This definition is ane manner to say what about all of us remember of distance intuitively, simply it is not the only manner we could talk about distance. You will meet in the following sections how the concept of altitude can be extended beyond length, in more than than one sense that is the breakthrough behind Einstein's theory of relativity.

If we stick with the geometrical definition of distance we nonetheless have to define what kind of space we are working in. In most cases, y'all're probably talking most iii dimensions or less, since that's all we can imagine without our brains exploding. For this calculator, we focus only on the 2d distance (with the 1D included equally a special case). If you lot are looking for the 3D distance between two points we encourage y'all to employ our 3D distance calculator made specifically for that purpose.

To detect the altitude between two points, the first matter you need is two points, plain. These points are described by their coordinates in space. For each point in 2d infinite, we demand two coordinates that are unique to that point. If yous wish to find the distance betwixt two points in 1D space you can still utilise this calculator by but setting one of the coordinates to be the same for both points. Since this is a very special case, from now on we will talk only almost distance in two dimensions.

The side by side step, if you want to be mathematical, accurate, and precise, is to define the type of infinite you're working in. No, await, don't run abroad! Information technology is easier than yous think. If you don't know what space you're working in or if you didn't even know at that place is more than ane type of space, yous're about likely working in Euclidean space. Since this is the "default" space in which nosotros do almost every geometrical operation, and it's the one nosotros take set for the figurer to operate on. Let's dive a bit deeper into Euclidean space, what is it, what properties does it take and why is it and then of import?

The distance formula for Euclidean distance

The Euclidean space or Euclidean geometry is what nosotros all unremarkably think of 2nd space is before we receive any deep mathematical training in any of these aspects. In Euclidean space, the sum of the angles of a triangle equals 180º and squares have all their angles equal to 90º; always. This is something we all take for granted, just this is not truthful in all spaces. Permit'southward also not misfile Euclidean space with multidimensional spaces. Euclidean space can have equally many dimensions as you lot want, as long every bit in that location is a finite number of them, and they still obey Euclidean rules.

We do not want to bore you with mathematical definitions of what is a infinite and what makes the Euclidean space unique, since that would be as well complicated to explain in a simple altitude calculator. However, we can try to requite you some examples of other spaces that are normally used and that might help you lot sympathize why Euclidean space is non the just space. Also, you will hopefully empathise why we are not going to bother computing distances in other spaces.

The first example we nowadays to you is a bit obscure, but we promise yous can excuse us, as nosotros're physicists, for starting with this very important type of space: Minkowski infinite. The reason we've selected this is considering it's very common in physics, in detail it is used in relativity theory, general relativity and even in relativistic breakthrough field theory. This space is very similar to Euclidean infinite, but differs from it in a very crucial feature: the addition of the dot product, as well called the inner product (not to be confused with the cross production).

Both the Euclidean and Minkowski infinite are what mathematicians telephone call flat infinite. This means that space itself has flat properties; for example, the shortest distance betwixt whatsoever two points is always a direct line betwixt them (bank check the linear interpolation estimator). There are, all the same, other types of mathematical spaces chosen curved spaces in which space is intrinsically curved and the shortest distance betwixt ii points is no a straight line.

This curved space is hard to imagine in 3D, but for second we can imagine that instead of having a apartment plane surface area, we have a 2D space, for example, curved in the shape of the surface of a sphere. In this case, very strange things happen. The shortest altitude from one bespeak to another is not a straight line, because any line in this space is curved due to the intrinsic curvature of the space. Another very strange characteristic of this space is that some parallel lines do actually meet at some indicate. You can try to understand information technology by thinking of the and then-called lines of longitude that carve up the Earth into many time zones and cantankerous each other at the poles.

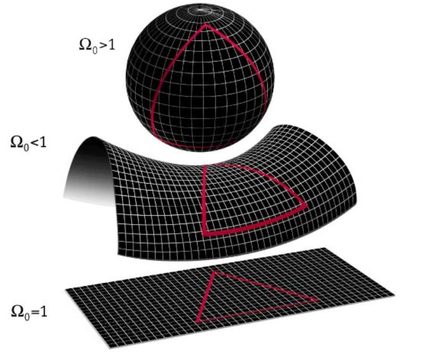
Information technology is of import to notation that this is conceptually VERY different from a change of coordinates. When nosotros take the standard 10, y, z coordinates and convert into polar, cylindrical, or even spherical coordinates, but we will yet be in Euclidean space. When we talk about curved space nosotros are talking near a very different space in terms of its intrinsic properties. In spherical coordinates, yous tin still accept a directly line and distance is still measured in a straight line, even if that would be very difficult to express in numbers.

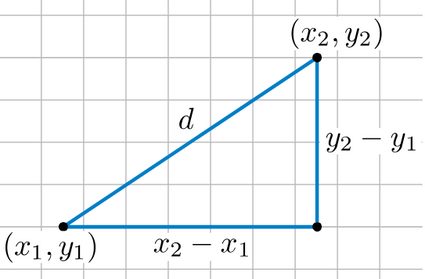
Coming back to the Euclidean space, nosotros can now present yous with the distance formula that we promised at the beginning. The distance formula is

√[(x₂ - ten₁)² + (y₂ - y₁)²],

which relates to the Pythagorean theorem: a² + b² = c². Hither, a and b are legs of a right triangle and c is the hypotenuse. Suppose that 2 points, (x₁, y₁) and (ten₂, y₂), are coordinates of the endpoints of the hypotenuse. Then (x₂ - 10₁)² in the distance equation corresponds to a² and (y₂ - y₁)²corresponds to b². Since c = √(a² + b²), you tin can see why this is just an extension of the Pythagorean theorem.

An extended application of the distance between points can be constitute in the segment addition postulate, which involves finding a segment length when iii points are collinear.

Distance to any continuous structure

The distance formula we take just seen is the standard Euclidean distance formula, but if you think virtually it, information technology can seem a fleck limited. We often don't want to find just the distance between two points. Sometimes we want to calculate the distance from a point to a line or to a circle. In these cases, we first demand to ascertain what point on this line or circumference we will use for the altitude adding, and then utilize the distance formula that we have seen simply higher up.

Hither is when the concept of perpendicular line becomes crucial. The distance betwixt a point and a continuous object is defined via perpendicularity. From a geometrical betoken of view, the first step to mensurate the distance from one point to another, is to create a directly line between both points, and so mensurate the length of that segment. When we measure out the distance from a betoken to a line, the question becomes "Which of the many possible lines should I draw?". In this case the answer is: the line from the betoken that is perpendicular to the first line. This distance will be goose egg in the instance in which the point is a part of the line. For these 1D cases, we can only consider the altitude between points, since the line represents the whole 1D space.

This imposes restrictions on how to compute distances in some interesting geometrical instances. For instance, we could redefine the concept of elevation of a triangle to exist only the distance from 1 vertex to the opposing side of the triangle. In this case, the triangle area gets likewise redefined in terms of distance, since the expanse is a function of the meridian of the triangle.

Distance to a line and between ii lines

Allow's look at couple examples in second space. To calculate the distance between a point and a directly line we could go footstep by pace (summate the segment perpendicular to the line from the line to the point and the compute its length) or we could simply use this 'handy-dandy' equation: d = |Ax1 + Pasti + C | / √(Aii + B2) where the line is given by Ax+Past+C = 0 and the point is defined by (xone, y1).

The only problem hither is that a straight line is generally given every bit y = mx + b so we would need to convert this equation to the previously show form: y = mx + b → mx - y + b = 0 and then we can come across that A = thousand, B = -1 and C = b. This leaves the previous equation with the following values: d = |mx1 -y1 + b | / √(m2 + ane).

For the distance betwixt 2 lines, nosotros merely need to compute the length of the segment that goes from one to the other and is perpendicular to both. Once once again, there is a elementary formula to assist the states: d= |C2-C1|/√(A2+B2) if the lines are A1 x+B1 y+C1 = 0 and A2x+Biiy+C2 = 0. We tin can besides convert to gradient intercept for and obtain: d= |btwo-bone|/√(yard2+1) for lines y = monex + b1 and y = thoutwox + b2 .

Notice that both line needs to be parallel since otherwise the would touch at some point and their distance would then be d = 0. That's the reason the formulas omit virtually of the subscripts since for parallel lines: A1 = A2 = A and Bone = B2 = B while in gradient intercept form parallel lines are those for which grand1 = yard2 = m

Autonomously from perpendicularity, another important concept to talk about regarding distance, is the midpoint. This is the betoken that is precisely in the middle between the two others. The midpoint is divers as the point that is the same distance away from each of the points of reference. We can and will generalize this concept in a later section, simply for now, we can limit ourselves to geometry. For instance, the midpoint of any bore in a circumvolve or even a sphere is always the middle of said object.

How to find the distance using our altitude calculator

As nosotros have mentioned before, distance tin hateful many things, which is why we have provided a few unlike options for you in this calculator. You lot can calculate the distance between a point and a straight line, the distance betwixt two direct lines (they always accept to exist parallel), or the distance between points in infinite. When it comes to computing the distances between ii bespeak, you have the selection of doing and then in one, 2, iii, or 4 dimensions. I know, I know, 4 dimensions sounds scary, merely you don't need to use that option. And you tin always learn more most it past reading some dainty resource and playing effectually with the calculator. We promise it won't break the Net or the universe.

We have also added the possibility for you to define three different points in infinite, from which you will obtain the iii pairs of distances between them, so, if yous take more than two points, this will save y'all time. The number of dimensions you are working in will determine the number of coordinates that describe a bespeak, which is why, as y'all increase the number of dimensions, the figurer will ask for more input values.

Even though using the calculator is very straightforward, we still decided to include a footstep-by-step solution. This way you lot tin get acquainted with the altitude formula and how to utilize it (as if this was the 1950'south and the Cyberspace was nonetheless non a thing). Now let's have a look at a applied instance: How to find the altitude between two points in 2-D.

Suppose y'all have two coordinates, (3, five) and (9, 15), and you desire to calculate the distance between them. To summate the ii-D distance between these 2 points, follow these steps:

1. Input the values into the formula: √[(10₂ - 10₁)² + (y₂ - y₁)²].
2. Subtract the values in the parentheses.
3. Foursquare both quantities in the parentheses.
4. Add together the results.
5. Take the square root.
6. Utilize the distance figurer to check your results.

Working out the example by manus, you get:

√[(9 - 3)² + (15 - 5)²] = √[(6)² + (10)²] = √[36 + 100] = √136,

which is equal to approximately xi.66. Note, that when y'all have the square root, you will go a positive and negative result, just since y'all are dealing with altitude, yous are only concerned with the positive result. The calculator volition go through this calculations step by step to requite you the result in verbal and approximate formats.

Driving distance between cities: a real-globe case

Let's take a await of one of the applications of the distance calculator. You lot can utilise it together with the gas calculator for making road trip plans. Suppose you are traveling between cities A and B, and the simply stop is in city C, with a route A to B perpendicular to route B to C. We tin can determine the distance from A to B, then, with the gas reckoner, make up one's mind fuel price, fuel used and cost per person while traveling.

The difficulty hither is to calculate the distances between cities accurately. A direct line (similar what nosotros use in this calculator) can be a good approximation, but it tin can be quite off if the route you're taking is non direct but takes some detour, maybe to avoid mountains or to laissez passer by some other city. In that case, just use Google maps or any other tool that calculates the distance along a path not just the distance from one indicate to another as the crow flies.

Where our calculator tin give proper measurements and predictions, is when calculating distances between objects, not the length of a path. With this in mind, there are still multiple scenarios in which you lot might actually be interested in the distance between objects, regardless of the path you would have to take. 1 such example is the distance between astronomical objects.

Altitude from Earth to Moon and Dominicus - astronomical distances

When we look at a distance inside our World, information technology is difficult to get in without bumping into some problems, from the intrinsic curvature of this space (due to the Earth curvature being non-zero) to the express maximum distance between ii points on the Earth. It is because of this, and besides because there is a whole universe across our Globe, that distances in the universe are of big interest for many people. Since we have no proper ways of interplanetary traveling, let alone interstellar travels, allow's focus for now on the actual Euclidean distance to some celestial objects. For case the distance from the World to the Sun, or the distance from the Earth to the Moon.

These distances are beyond imaginable for our ape-similar brains. We struggle to comprehend the size of our planet, never mind the vast, infinite universe. This is then difficult that we demand to utilize either scientific notation or low-cal years, equally a unit of altitude for such long lengths. The longest trips you can do on World are barely a couple one thousand kilometers, while the distance from Globe to the Moon, the closest astronomical object to the states, is 384,000 km. On top of that, the distance to our closest star, that is the distance from Earth to the Dominicus, is 150,000,000 km or a piddling over eight light minutes.

When you compare these distances with the distance to our 2nd nearest star (Alpha Centauri), which is four lite years, suddenly they kickoff to look much smaller. If we want to go even more ridiculous in comparison we can always retrieve near a flying from New York to Sydney, which typically takes more than than 20 h and it's only over 16,000 km, and compare it with the size of the observable universe, which is about 46,600,000,000 lite years !

Hither, nosotros have inadvertently risen a fascinating signal, which is that we measure distances not in length but in time. Thus, nosotros extend the notion of altitude beyond its geometrical sense. We will explore this possibility in the next section as we speak about the importance and usefulness of distance beyond the purely geometrical sense. This is a very interesting path to accept and is mostly inspired by the philosophical demand to extend every concept to accept a universal significant, as well as from the obvious physical theory to mention, when talking well-nigh permutations of the space and time, or any other variable that can be measured.

Altitude beyond length

Typically, the concept of distance refers to the geometric Euclidean distance and is linked to length. All the same, you can extend the definition of altitude to hateful merely the difference between two things, and and so a world of possibilities opens upwardly. All of a sudden one can make up one's mind what is the best mode to measure out the distance between ii things and put information technology in terms of the most useful quantity. A very unproblematic stride to take is to think about the distance between ii numbers, which is nix more than the 1D difference betwixt these numbers. To obtain it, nosotros simply subtract one from the other and the result would be the difference, a.yard.a. the altitude.

We could bound from this numerical altitude to, for example, difference or altitude in terms of the percent departure, which in some cases might provide a better manner of comparison. Nosotros don't need to stay just with percentage, nosotros can convert percentage to fraction if you lot feel that would exist the best way to express altitude. Just so far, this is nonetheless just one level of abstraction in which we simply remove the units of measurement. But what if we were to use dissimilar units altogether?

By extending the concept of distance to mean something closer to departure, we can calculate the difference between two temperatures in terms of degrees or thermal energy, or other related quantity like pressure. Just we don't demand to become really extreme, let's meet how two points can be separated by a dissimilar distance, depending on the assumptions made. Coming back to the driving distance example, we could measure the distance of the journey in time, instead of length. In this case, we demand an assumption to let such translation; namely the style of transport.

There is a big difference in the time taken to travel 10 km by plane versus the time it takes past machine; or by car versus cycle. Sometimes, all the same, the assumption is clear and implicitly agreed on, like when we measure the lightning distance in fourth dimension which nosotros and so convert to length. This brings up an interesting betoken, that the conversion factor between distances in fourth dimension and length is what we telephone call speed or velocity (remember they are not exactly the aforementioned thing). Truth be told, this speed doesn't have to be constant as exemplified by accelerated motions such equally that of a complimentary fall nether gravitational force, or the one that links stopping time and stopping distance via the breaking force and drag or, in very extreme cases, via the strength of a machine crash.

Some other place where yous can find weird units of distance are in solid country physics, where the distance a particle travels within of a textile is often expressed every bit an average of interactions or collisions. This distance is linked to length by using the mean gratuitous path which is the mean distance (in length) a particle travels between interactions. If nosotros want to get fifty-fifty more exotic we can think almost the distance from the nowadays value to the future value of something like a car. This altitude between prices is linked here by the car depreciation, and it'due south not equally cutting and dry out as the other distances, but only because of the number of factors involved in calculating this distance.

We don't want to, however, make anyone'due south encephalon explode, then please don't think besides hard about this. Just take this calculator and use it for length-based distance in 2D space. Yous can always return to this philosophical view on distances if you ever find yourself bored and having already checked all of our Omni Calculators.

FAQ

How to notice the distance between ii points?

To find the distance between two points we will employ the distance formula: √[(x₂ - ten₁)² + (y₂ - y₁)²]

1. Get the coordinates of both points in infinite
2. Decrease the x-coordinates of ane signal from the other, same for the y components
3. Foursquare both results separately
4. Sum the values you got in the previous step
5. Find the square root of the result above.

If you lot call back this is besides much effort y'all tin can simply utilise the Distance Calculator from Omni

Is distance a vector?

Altitude is not a vector. The distance between points is a scalar quantity, significant it is merely defined by its value. Nevertheless, the deportation is a vector with value and management. So the distance between A and B is the same as the altitude from B to A, just the displacement is different depending on their gild.

What is a click in altitude?

Click is slang for a kilometer which is 0.62 miles. It is actually written with "one thousand" (Klick) as information technology is derived from the give-and-take kilometer. Information technology is commonly used in the military and motorcyclists.

What is the distance formula?

The distance formula is: √[(x₂ - x₁)² + (y₂ - y₁)²]. This works for any 2 points in second space with coordinates (x₁, y₁) for the first point and (10₂, y₂) for the second point. You tin can memorize it easily if you notice that it is Pythagoras theorem and the distance is the hypothenuse, and the lengths of the catheti are the divergence between the x and y components of the points.

How to find the distance of a vector?

The distance of a vector is its magnitude. If you know its components:

1. Take each of the components of the vector and square them
2. Sum them up
3. Detect the square root of the previous event
4. Savor the skilful work!

If y'all know its polar representation, it will be a number and an bending. That number is the magnitude of the vector, which is its distance.

What is the SI unit of measurement of distance?

The SI unit of measurement of distance is the meter, abbreviated to "m". A meter is approximately iii.28 feet. Other common units in the International System of units are the centimeter (one i-hundredth of a meter, or 0.39 inches) and the kilometer (one thou meters or 0.62 miles), among others.

What is the distance from a to b?

The distance from A to B is the length of the straight line going from A to B. The altitude from B to A is the same as the distance from A to B because distance is a scalar

What is the dimension of distance?

Distance is a mensurate of one-dimensional space. The distance between two points is the shortest length of 1D space betwixt them. If y'all divide distance over fourth dimension you will go speed, which has dimensions of space over time.

Is light-year fourth dimension or distance?

A lite-year is a measurement of distance. It is 9.461⨉x¹² kilometers or 5.879⨉10¹², which is the distance traveled past a ray of light in a perfect vacuum over the span of a year.

How to solve for altitude with velocity and time?

The velocity and the moving time of an object you can calculate the distance:

1. Make certain the speed and time have compatible units (miles per hour and hours, meter per second, and seconds...)
2. If they aren't, convert them to the necessary units
3. Multiply the velocity past the time
4. The upshot should exist the distance traveled in whichever length units your speed was using!

Source: https://www.omnicalculator.com/math/distance

Posted by: singhfattle.blogspot.com

Share this post